VOCABULARIO
Places:
school--- cinema--- supermarket--- bookshop--- restaurant--- clothes shop--- pool--- bank--- police station--- park
Rooms of the House:
Bedroom- bathroom- living-room--- dining room---kitchen--- hall
EJERCICIOS PAGS 13-14
GRAMÁTICA
Conjugación del presente simple. (Present Simple)
Cojamos el verbo WORK como ejemplo:
AFFIRMATIVE NEGATIVE INTERROGATIVE
I work I don't work Do I work?
You work You don't work Do you work?
He works He doesn't work Does he work?
She works She doesn't work Does she work?
It works It doesn't work Does it work?
We work We dont't work Do we work?
You work You don't work Do you work?
They work They don't work Do they work?
* Reglas para añadir -s en 3ª persona del singular:
1. La mayoría de los verbos añaden -s sin que haya ningún cambio: work-works
2.Los verbos acabados en -s, -sh, -ch, -x, o -o, añaden -es: wash-washes/watch-watches/go-goes
3.Los verbos acabados en consonante+y, cambian "y" por "i" y añaden -es: study-studies
4.Los verbos acabados en voca+y, añaden -s sin que haya ningún cambio: play-plays
5.El verbo have en 3ª persona se convierte en "has"
EJERCICIOS PAGS. 40-41-42-43-44
Matemáticas
Comenzamos tema: Potencias
Ejercicios pág 8
Ejercicios pág 9, 10, 11, 12 y 13
Lengua
Corregimos ejercicios del tema del léxico para comenzar el de categorías gramaticales.
Tipos de palabras o Categorías gramaticales:
- Sustantivos o nombres. Palabras variables (tienen género y número) que sirven para nombrar seres, objetos, ideas, etc. Según su significado, pueden ser: propios o comunes, concretos o abstractos, individuales o colectivos.
- El adjetivo. Es una palabra variable que expresa una cualidad o propiedad de lo que designa el sustantivo Grados del adjetivo: – positivo: el adjetivo aparece sin modificar su significado. Alto
- Los adjetivos pueden ser:
- -Calificativos (si la cualidad que designan se puede graduar) - (listo - muy listo)
- -Relacionales (si la cualidad que designan no se puede graduar) (español -
- Haz todos los ejercicios del tema referidos al adjetivo
SEMANA DEL 13 AL 17 DE MARZO
Inglés
VOCABULARIO
Numbers:
Dado que en el temario se muestra el vocabulario de las decenas conviene repasar los números
ten---twenty---thirty---forty---fifty---sixty---seventy---eighty---ninety---a hundred
Clothes:
jumper---dress---skirt---hat---trousers---socks---jacket---shirt---jeans---trainers---shoes---tracksuit
Ejercicios pág 11 y 12
GRAMÁTICA
- Aprende el uso del artículo síngular (a / an)
(Ejemplos: a car, a boy, a girl)
Recuerda que la letra h en inglés se pronuncia, con lo cual se considera una consonante la mayoría de las veces (a hospital)
De la misma forma, algunas palabras que comienzan por u se considera que comienzan por consonante por motivos de pronunciacion. (Ejemplo a university - una universidad)
-An se puede traducir por (un/una y se usa cuando el nombre que le sigue empieza por vocal
(Ejemplos: an elephant, an orange, an apple)
Recuerda también el caso de "una hora" (an hour) - En este caso la h no se pronuncia por eso se considera que la palabra empieza por vocal
Ejercicios pág. 36
Nos adentramos en el siguiente tema: LAS FRACCIONES
Matemáticas
Nos adentramos en el siguiente tema: LAS FRACCIONES
|
SEMANA DEL 6 AL 10 DE MARZO
Inglés
VOCABULARIO
Parts of the body:
leg----teeth---head---finger----arm----mouth---ear----hair----toe---eye---foot----nose
Pets:
duck---turtle---cat---dog---fish---bird---hamster---rabbit---snake
Food:
apple----banana-----vegetables-----sweets-----meat----bread---pizza-----cheese----biscuits----orange juice----milk---chips-----fish------hamburger
Ejercicios 7, 8 y 9
GRAMÁTICA
Ejercicios páginas 34 y 35
Lengua
Comenzamos el siguiente bloque correspondiente a la TIPOLOGÍA TEXTUAL.
FORMAS DE LA COMUNICACIÓN ORAL Y ESCRITA
1.1. Situaciones de la comunicación oral
La comunicación oral es aquella que se produce sin la presencia de elementos escritos. Deberá incorporar los elementos de la comunicación: emisor, receptor, mensaje, canal, código y contexto. En este caso la comunicación humana se desarrolla mediante un código sonoro y audible.
Por ese motivo, si no entendemos dicho código, no entenderemos el idioma y por lo tanto será imposible comunicarnos con otras personas que hablen idiomas distintos. Finalmente aclarar que para que exista comunicación tiene que haber mensaje de retorno o interacción entre emisor y receptor.
1.1.1.La exposición oral
Consiste en la transmisión de un mensaje largo ante un auditorio indeterminado. Hay que procurar que la exposición oral sea interesante y resulte amena. La exposición oral en el ámbito académico tiene una estructura: introducción (saludar y presentarse al auditorio, presentación del tema), desarrollo (diferenciando datos de opiniones, aportando ejemplos o anécdotas) y conclusión (resumiendo lo tratado, aportando soluciones o alternativas, y dando las gracias).
1.1.2. La narración oral
La narración oral no tiene un carácter académico tan acusado como la exposición oral. Tanto si es una narración improvisada como una narración preparada previamente, tendremos en cuenta estas consideraciones: no entretenerse en sucesos sin importancia, poner énfasis en momentos interesantes subiendo el tono de voz y acelerar el ritmo o disminuirlo según sean situaciones dinámicas o lentas respectivamente. Respecto de cuestiones lingüísticas, en la narración oral utilizaremos adverbios de tiempo y locuciones temporales, adverbios de lugar (precisión al expresar momento, dirección o localización) y adjetivos para precisar en las descripciones.
1.1.3. El lenguaje de la radio y la televisión
Las formas de comunicación oral más desarrolladas en los últimos decenios y con mayor éxito son la radio y la televisión. La radiodifusión se utiliza como medio para transmitir información y también permite la participación del oyente.
1.1.4. Ejemplos de expresión y comprensión de textos orales
Son muchos los ejemplos en los cuales el ser humano emplea diversos textos que toman su forma oral cuando expresan y se comprenden a través del canal sonoro y auditivo. Así, en este contexto, nos encontramos desde una simple conversación o una discusión, hasta expresiones más complejas y preparadas como un coloquio o un debate, en los cuales puede aparecer la figura del moderador (un intermediario entre emisor y receptor).
Ejemplos especiales de estas realizaciones orales son la recitación y la dramatización.
1.2. La interpretación de textos escritos
La lectura expresiva de los textos escritos tiene como principal característica que el lector lo hace en voz alta y para otras personas. La lectura expresiva es el arte de leer en público, para transmitir los pensamientos de unos para otros, por lo que bien enfocada, significa compartir el placer de la lectura.
Para conseguir una correcta realización tendremos en cuenta los siguientes aspectos al combinar el texto escrito con la lectura oral:
• Las pausas que vienen determinadas por el ritmo de la respiración y los signos de puntuación. Otras veces se realizan en función del sentido del texto.
• Los tonemas son el resultado del tipo de entonación con que se emiten los grupos fónicos (las realizaciones fónicas entre pausas), que a su vez pueden ser descendentes, ascendentes y horizontales. A su vez se relacionan con los tipos básicos de oraciones: afirmativas, negativas e interrogativas.
1.2.1. La comprensión de textos escritos
Es muy importante la exactitud de los significados de los textos escritos que leemos. En cualquier caso hay que ser crítico con el contenido del mensaje. El mensaje puede ser muy variado, pero especialmente el contenido publicitario e ideológico debe ser entendido en su totalidad.
1.2.2. Redacción y composición de textos escritos expositivos y argumentativos.
Existe gran variedad de textos escritos, aunque en este punto nos fijaremos en los textos expositivos y argumentativos.
En el caso de los textos expositivos se utilizan para presentar información sobre un tema de forma que sea entendida por los lectores. Ello significa utilizar un lenguaje comprensible para las personas a las que van dirigidos. Es importante que el texto esté contrastado, sea veraz y posea coherencia, y una estructura clarificadora de los contenidos.
El texto argumentativo tiene como finalidad defender ideas, pensamientos y opiniones, para lo cual debemos razonar y fundamentar nuestras ideas de forma que resulten convincentes. El texto argumentativo se estructura en tres partes: presentación de las ideas que se defienden, cuerpo de la argumentación y los razonamientos, y conclusión o resumen de las ideas defendidas.
ACTIVIDADES PÁGINA 19
Matemáticas
Nos adentramos en el siguiente tema: LAS FRACCIONES
|
Matemáticas
Semana dedicada a terminar los ejercicios del primer tema.
TEMA 2: POTENCIAS
| 1. Potencias de un número entero | |
¿Qué es una potencia?
Una potencia cuya base es un número entero y cuyo exponente es un número natural, es un producto de factores iguales.
La base, 5, es el factor que se repite. El exponente,2, indica el número de veces que se repite la base. Por ejemplo:
Potencias con base un número entero negativo
Al calcular potencias, ten cuidado si aparecen números negativos. Deberás decidir si el exponente afecta al signo o no, y si el resultado será negativo o positivo.
Vamos a estudiar el signo de una potencia. Después pulsa y haz algunos ejercicios para comprobar tus conocimientos.
Eso sí, puedes ir ya pensando en lo siguiente:
Ejercicios pág 11
Multiplicación y división de dos potencias del mismo exponente
|
Potencia de otra potencia
Ejercicios pág 12 y ejercicios de autoevaluación pág 13.
Lengua
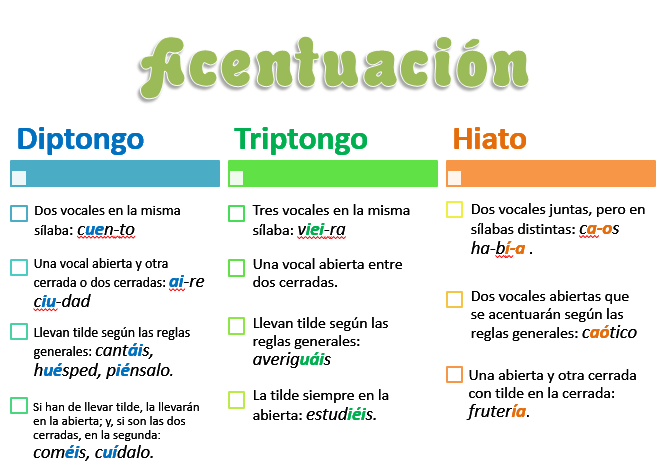
Continuamos la acentuación estudiando qué son los diptongos, triptongos e hiatos.
A continuación realiza los ejercicios 4 y 5 del tema.
Los ejercicios posteriores de ortografía han de hacerse en tiempo libre que tengáis en casa. Cualquier duda aclaramos en clase.
Inglés
VOCABULARIO
Adjectives of Description:
tall---short---old---young----fat-----thin----big----small----long----short---happy----sad
Realiza los ejercicios de la página 6
GRAMÁTICA
Continuamos con otro verbo a estudiar: HAVE GOT. Este verbo significa tener y aquí abajo puedes encontrar sus estructuras.
A continuación realizamos los ejercicios del libro correspondientes páginas 30-31-32-33
Matemáticas
Empezamos el tema 1: LOS NÚMEROS ENTEROS.
1. Concepto de número entero.
Los números enteros son una ampliación de los naturales:
Los naturales se consideran enteros positivos (se escriben con el signo +).
Los enteros negativos van precedidos del signo -.
El cero es un entero pero no es ni negativo ni positivo.
Ejemplos: No es lo mismo Tener 300€ (+300) que deber 300€ (-300)
Tener 38 grados de fiebre (+38) que estar a 3 grados bajo cero (-3)
2. La recta numérica.
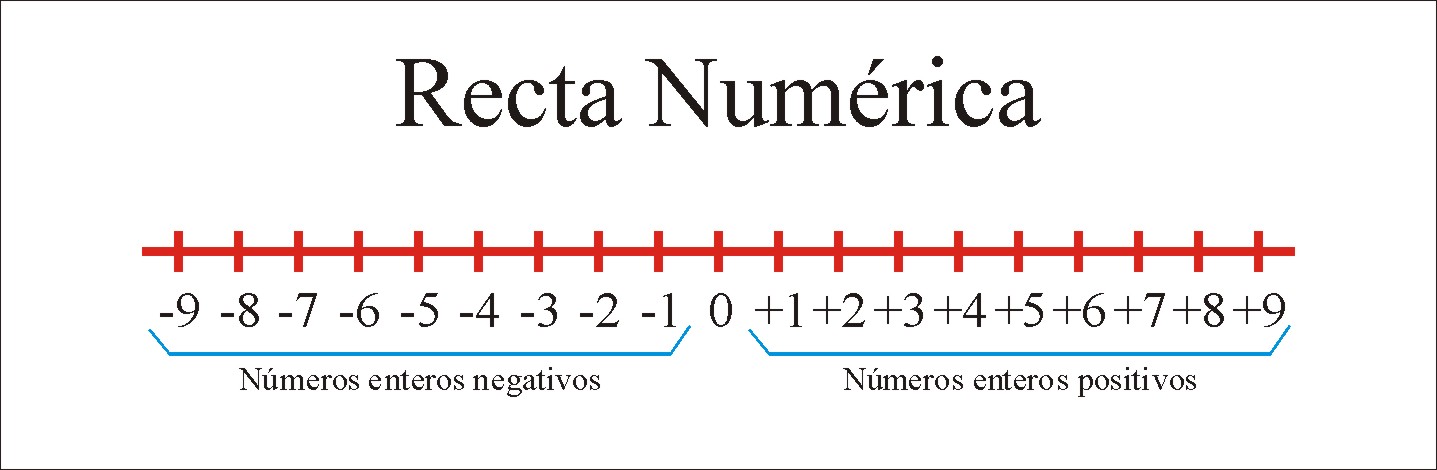
3. Valor absoluto.
El valor absoluto de un número entero es la distancia que le separa del cero.
Se escribe entre dos barras | | y es el número sin su signo:
|+a| = a |-a| = a
Se escribe entre dos barras | | y es el número sin su signo:
|+a| = a |-a| = a
El valor absoluto es una distancia por lo que no puede ser negativo.
Ej: |+5| = 5 |-5| = 5
4. Opuesto de un número entero.
El opuesto de un número entero es su simétrico respecto del cero.Se escribe así:
Op(+a) = -a Op(-a) = +a Ej: Op(+7)= -7
Op(+a) = -a Op(-a) = +a Ej: Op(+7)= -7
Op (-8)= +8
5. Suma y diferencia de números enteros.
Para sumar números enteros que tengan el mismo signo, positivo o negativo, se suman sus valores absolutos y se pone al resultado el signo de los sumandos. En caso de tener signos diferentes se restan los valores absolutos y se pone el signo del mayor.
- +6 +3 = +9
significa que tienes 6 y te dan 3
=> tienes 9 - -7 -5 = -12
significa que debes 7 y gastas 5
=> acumulas una deuda de 12 - -6 +8 = +2
significa que tienes 8 pero debes 6
=> tienes 2 El dinero supera las deudas - -5 +3 = -2
significa que debes 5 y tienes 3
=> debes 2 Las deudas superan el dinero.
Cuando tres o más números enteros tenemos dos métodos:
1) agrupar los dos primeros sumandos y sumar al resultado el tercer sumando
+6 -4 +3 = +2 +3 = +5
En el caso de 4 sumandos se puede agrupar
de dos en dos:
+6 -4 +3 -2 = +2 +1 = +3
+6 -4 +3 = +2 +3 = +5
En el caso de 4 sumandos se puede agrupar
de dos en dos:
+6 -4 +3 -2 = +2 +1 = +3
2) sumar los positivos por un lado (tener) y los
negativos (deber) por el otro y finalmente
hallar el resultado
deber tener
-7 +8 -5 = -12 +8 = -4 deber tener
negativos (deber) por el otro y finalmente
hallar el resultado
deber tener
-7 +8 -5 = -12 +8 = -4 deber tener
+6 -4 +3 -2 = -6 +9 = +3
Expresiones sencillas con paréntesis en la suma y la resta: Debemos tener en cuenta el signo que hay delante de un paréntesis.
+ (+a) = +a - (+a) = - a
+ (- a) = - a - (- a) = +a
+ (- a) = - a - (- a) = +a
6.
6. Multiplicación y División de números enteros.
Producto de enterosPara hallar el producto de dos números enteros:
- se multiplican los dos nº sin signo
- aplicamos la regla de los signos
División de enterosPara hallar la división de dos números enteros:
- se dividen los dos nº sin signo
- aplicamos la regla de los signos
 | Si los dos nº son del mismo signo el producto es positivo. |
Si tienen distinto signo el producto es negativo.
|
7. Prioridad en las operaciones.
Siempre que tengamos operaciones combinadas de sumas, restas, multiplicaciones y divisiones, hay que realizarlas en el siguiente orden.
1º- Paréntesis y corchetes de dentro hacia fuera.
2º- Multiplicación y división en el orden en que aparecen.
3º- Suma y resta en el orden en que aparecen.
UNA VEZ ESTUDIADO EL TEMA REALIZA LOS SIGUIENTES EJERCICIOS DEL TEMA:
PÁG. 1 Ordenar y expresar en números enteros.
PÁG. 2 Representar en la recta, valor absoluto, sumas y opuestos.
PÁG. 3 Sumas y restas combinadas.
Lengua
Comenzamos el primer tema dedicado a la ORTOGRAFÍA. En este tema tendréis que trabajar los ejercicios a partir del punto 2 por vuestra cuenta. De esta forma comenzamos con el punto 1 en clase:
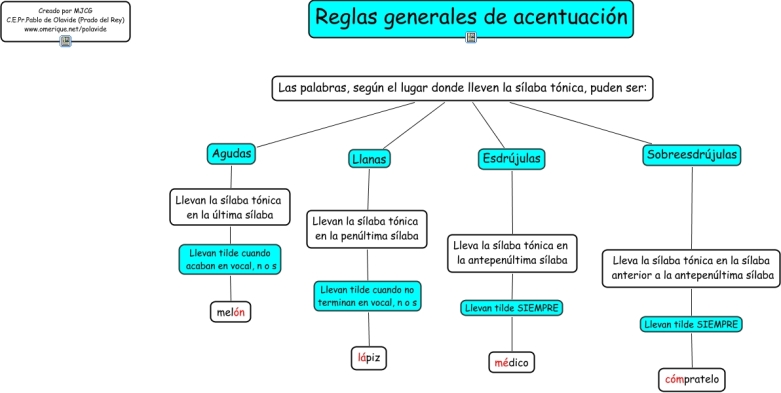
1. Las reglas generales de acentuación
Podríamos definir el acento como la mayor intensidad con que pronunciamos una sílaba dentro de una palabra. La definición de acento no coincide con la de tilde: mientras el primero es una marca fónica, la tilde es un signo gráfico.
De este modo, según la sílaba donde recaiga el mayor golpe de voz dentro de una palabra, tendremos distintos grupos de palabras:
- Palabras agudas. Son las que tienen el acento en la última sílaba y llevan tilde siempre que acaben en vocal, -n o -s: café, riñón, compás...
- Palabras llanas. Son las que tienen el acento en la penúltima sílaba y llevan tilde siempre que no terminen en vocal, -n o -s: fácil, difícil, lápiz....
- Palabras esdrújulas y sobreesdrújulas. Son aquellas que tienen el acento en la antepenúltima sílaba o en la anterior a la antepenúltima y siempre llevan tilde: Ángela, hipopótamo, rápido, cántaro....
En el caso de las letras mayúsculas siempre han de llevar tilde.
HAZ LOS EJERCICIOS 1 Y 2 DE LA PÁG. 4.
Acabamos el punto de las normas de acentuación estudiando los diptongos, triptongos e hiatos asi como la tilde en los monosílabos.
Inglés
- Aprende el verbo to be (ser o estar en castellano) en sus formas afirmativa y negativa
Affirmative
I am (I'm)
You are (You're)
He is (He's)
She is (She's)
It is (It's)
We are (We're)
You are (You're)
They are (They're)
Negative
I am not (I'm not)
You are not (You aren't)
He is not (He isn't)
She is not (She isn't)
It is not (It isn't)
We are not (We aren't)
You are not (You aren't)
They are not (They aren't)
- Practica. Realiza este ejercicio y este otro
Interrogative
Am I?
Are you?
Is he?
Is she?
Is it
Are we?
Are you?
Are they
- Practica con este ejercicio y este otro
En cuanto a vocabulario:
Family: dad-----mum-----brother------sister--------baby--------dog
En la página 4 del libro encontrarás ejercicios para trabajarlo
Classroom:
book----notebook-----pencil-----student-----schoolbag----pen-----ruler---- rubber----blackboard-----teacher
Ejercicios página 5







.jpg)








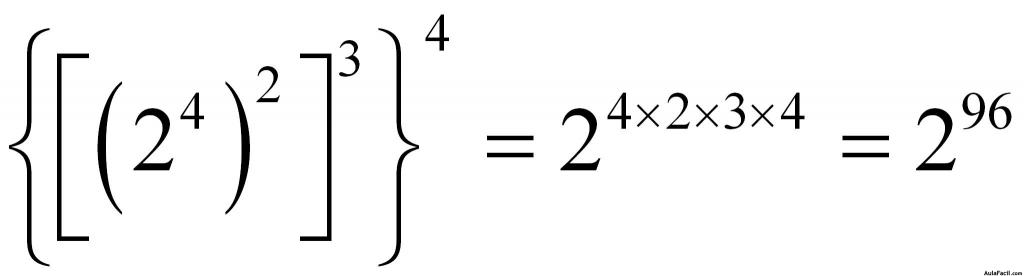





No hay comentarios:
Publicar un comentario